微软2017年预科生计划在线编程笔试 第1题 Legendary Items

题目1 : Legendary Items

时间限制:10000ms
单点时限:1000ms
内存限制:256MB

描述

Little Hi is playing a video game. Each time he accomplishes a quest in the game, Little Hi has a chance to get a legendary item.

At the beginning the probability is P%. Each time Little Hi accomplishes a quest without getting a legendary item, the probability will go up Q%. Since the probability is getting higher he will get a legendary item eventually.

After getting a legendary item the probability will be reset to ⌊P/(2I)⌋% (⌊x⌋ represents the largest integer no more than x) where I is the number of legendary items he already has. The probability will also go up Q% each time Little Hi accomplishes a quest until he gets another legendary item.

Now Little Hi wants to know the expected number of quests he has to accomplish to get N legendary items.

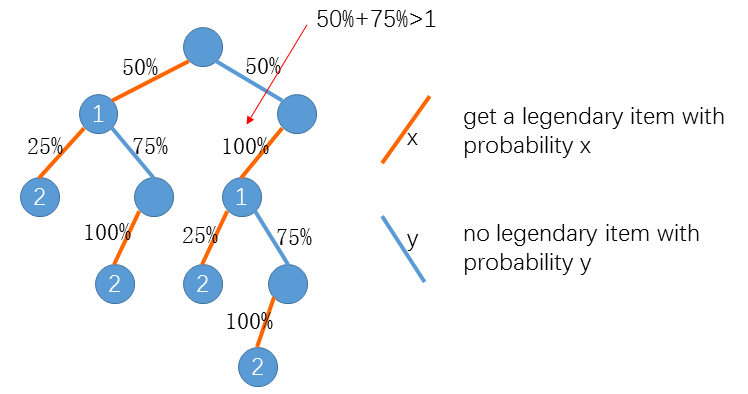
Assume P = 50, Q = 75 and N = 2, as the below figure shows the expected number of quests is 3.25

2*50%*25% + 3*50%*75%*100% + 3*50%*100%*25% + 4*50%*100%*75%*100% = 3.25

输入

The first line contains three integers P, Q and N.

$1 \leq N \leq 10^6, 0 \leq P \leq 100, 1 \leq Q \leq 100$

输出

Output the expected number of quests rounded to 2 decimal places.

---

样例输入

50 75 2

样例输出

3.25

---

解析

不得不承认，微软在样例中给的二叉树真的十分具有诱惑性，让人第一反应就是模仿这个样子去实现，去计算。为什么呢？
因为用二叉树表现这个概率计算过程，一看就明了，算法都很清晰，剩下的就是去码代码了。

但是，很显然，这样做和暴力解题是差不多的。
就是从N个传奇物品出发，思考所有的可能性，并计算每种可能性的概率。

最终通过数学期望的定义：
　　　$EX=\sum{(X \cdot P(X))}$

计算想要的结果。

首先，我们要看到的是，这是一道典型的概率计算题目。
每次完成任务，结果无非就是“获得传奇物品”和“未获得物品”。未获得物品时候，我们继续完成任务，这次获得的概率将会变化（不断提高），也就是说，最终必然会获得一个传奇物品。

在思考这个问题的时候，首先要很清晰的认识到每次获得传奇物品这个事件，是相互独立的。获得第一个传奇物品和获得第$i$个传奇物品是独立的，即便第$i$次的概率是通过$[P/2^i]$计算得到的，但实际上每次的$P'$(区别于初始$P$)都是固定的。

所以，在计算最终期望的过程中，我们就可以对每次获得传奇物品的任务期望分别计算，最后进行加和，即可得到最终的结果。

根据数学期望的性质：
　　　$E(X+Y)=EX+EY$

所以
$EN=E_{(1)}1+E_{(2)}1+E_{(3)}1+.....+E_{(N)}1$

而每次获得传奇物品的期望$E_{(i)}1$计算方法如下：

1.初始任务数（至少1次任务就能获得）$numQuests=1$
2.第一次任务对该次获得传奇物品增加的期望：$incE=(1-P)$
3.调整概率$P=P+Q$
4.进行下一次任务对该次获得传奇物品增加的期望计算：$incE=incE\cdot(1-P)$
5.任务期望：$numQuests=numQuest+incE$
6.回到步骤3
7.直至$P=P+Q>100$终止此次获得传奇物品的期望计算$numQuests$

---

其实这个代码还可以继续优化，因为在P小于一定值的的时候，后续的传奇物品的期望都是相同的。比如在$Q=75$时，$P<5$后，期望就相同了，不必重复计算。

---

AC代码（C++）：

#include<iostream>
#include<iomanip>

using namespace std;

int main()
{
	int P, Q, N;
	cin >> P >> Q >> N;

	double count_q=Q*1.00/100;
	double count_p;
	double result = 0.00;
	
	for (int i = 1; i <= N; i++)
	{
		double next_result = 1;

		count_p = P*1.00 / 100;
		double E1 = 1.00;
		while (1)
		{
			E1 = E1*(1.00 - count_p);
			next_result += E1;
			count_p += count_q;
			if (count_p > 1.00)
				break;
		}


		result += next_result;
		P = P / 2;
	}

	cout << fixed << setprecision(2) << result;

	return 0;
}

最终结果

编号	题目	结果	语言	时间	内存
1489	Legendary Items	AC	G++	22ms	0MB